3. razred
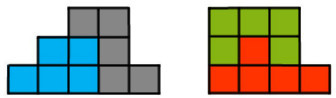
Naloga 1. Nejc ima 4 karte (glej sliko).
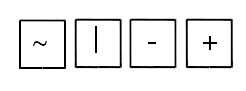
Odločil se je, da bo naredil različne vrstice, vsaka od katerih mora biti sestavljena iz vseh štirih kart. (Ena od njegovih vrstic je prikazana zgoraj)
Koliko različnih vrstic lahko dobi na tak način?
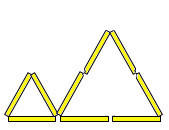
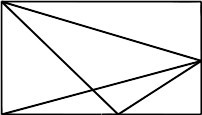
Naloga 2. Koliko trikotnikov je na sliki?
Naloga 3. En od 22 kovancev je ponarejen. Vsi pravi kovanci tehtajo enako, ponarejen pa je lažji od pravega. Imamo dvoramensko tehtnico (glej sliko).

Najmanj koliko tehtanj potrebujemo, da zagotovo najdemo ponaredek?
Naloga 4. V starem mestu je park, sredi parka pa jezero. Na jezeru so 3 otoki. Ti otoki so povezani z obalo jezera in drug z drugim z mostovi (glej sliko).
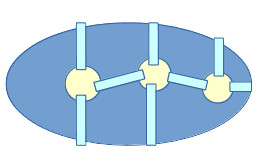
Ali se je mogoče sprehoditi skozi vse mostove z eno potezo, ne da bi šli dvakrat skozi isti most (lahko začnete pot tako od obale kot od katerega koli otoka)? Če je mogoče, kako? Če ne, zakaj?
Naloga 5. Pikapolonica se je usedla na plošči, ki je razdeljena na 9 kvadratnih celic.

Iz celice, na kateri je prikazana na sliki, se je premaknila mimo še treh celic in se ustavila na četrti. Premikala se je le naprej, nazaj, levo ali desno, vendar ne diagonalno. Označite vse celice, na katerih je lahko pikapolonica zdaj.
Naloga 6. Trije trikotniki so bili narejeni iz 9 palic (glej sliko).
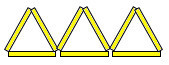
Premaknite le 2 palici tako, da bi na koncu dobili 2 trikotnika (vsaka palica mora biti del trikotnika).
Naloga 7. Daljica AB je dolga 9 cm. Na tej daljici smo narisali točko O. Izkazalo se je, da je daljica AO dvakrat krajša od daljice OB. Koliko je dolga daljica AO?
Naloga 8. V pritličju stoji 5 biciklov. Nekateri od njih so dvokolesni, nekateri pa trokolesni. Vemo, da imajo vsi bicikli skupaj 12 koles. Koliko dvokolesnih in koliko trokolesnih biciklov stoji v pritličju?
Naloga 9. Na ravni 10 kilometrov dolgi cesti so bile na eni strani postavljene svetilke v vrsti od samega začetka do konca ceste. Razdalja med dvema sosednjima svetilkama je 1 km. Koliko svetilk stoji ob cesti?
Naloga 10. Prileteli so ptiči in se usedli na veje stare breze. Če bi sedel na vsaki veji le po en ptič, potem en ptič ne bi dobil prostora. Če bi sedela na vsaki veji po dva ptiča, bi ostala ena veja prazna. Koliko ptičev je letelo in koliko vej je bilo na stari brezi?
Naloga 11. Na sliki 1 so prikazani liki »pentamino«. Beseda »pentamino« pomeni, da je vsak od teh likov sestavljen iz 5 enakih kvadratkov.
Slika 1
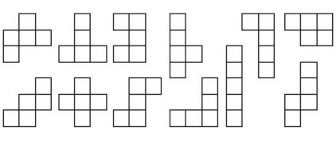
Imamo le po en pentamino vsake vrste. Iz nekaterih pentaminojev sestavite dva druga lika, ki sta prikazana na sliki 2. Pazite, da ne boste uporabili več kot en pentamino iste vrste.
Slika 2
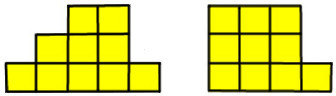
Naloga 12. Sonja je pobarvala svojo veliko kocko. Nato je od nje odstranila 4 majhne kocke in tako dobila figurico, ki je prikazana na sliki 1. S to figurico je na listu papirja naredila odtise. Katerih od odtisov, ki so prikazani na sliki 2, ne bi mogla narediti?
Slika 1

Slika 2
Naloga 13. Razrežite lik, ki je prikazan na sliki, vzdolž narisanih črt na tri pravokotnike. Vsi trije pravokotniki morajo biti različne velikosti.

Naloga 14. V čarobnem gozdu so živeli le zajci in lisice. Zajci so vedno govorili resnico, lisice pa laži. Zajci so se bali lisic, vendar se niso bali drugih zajcev, lisice pa se niso bali nikogar. Enkrat so se tri živali zbrale na jasi in se usedli v krogu. Vsaka žival je pogledala svojega soseda na desni in rekla: »Bojim se te!«
Koliko zajcev je bilo med njimi?