9. razred
Naloga 1. Ali je res, da lahko od katerih koli 100 naravnih števil zagotovo najdemo 15 takih, v katerih je razlika vsakega para števil deljiva s 7?
Naloga 2. Trikotnik je razdeljen na 25 enakih trikotnih celic (glej sliko).
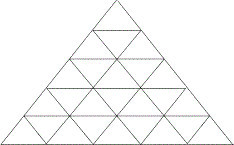
Pikapolonica se premika znotraj trikotnika in prehaja le med trikotnimi celicami, ki imajo eno skupno stranico. Katero je največje število celic, ki jih lahko pikapolonica obide, ne da bi bila v katerikoli od njih več kot enkrat? Dokažite, da je najdeno število maksimalno.
Naloga 3. Na tabli so zapisana vsa naravna števila od 1 do 1999 (1; 2; …; 1999). V eni potezi je dovoljeno izbrisati poljubno število števil in namesto njih napisati ostanek od deljenja njihove vsote z 11. Po nekaj potez sta se na tabli izkazali le dve števili, eno od katerih je 1000. Katero je drugo število?
Naloga 4. V eni tovarni je zaposleno 40 delavcev, od katerih je vsak umetnik, filozof ali pesnik. Skupaj je 28 umetnikov, 27 filozofov in 11 pesnikov. Katero je največje možno število delavcev, ki so istočasno in umetniki in filozofi?
Naloga 5. Koliko ničel ima število 100! na koncu?
Zapis n! je faktoriela (fakulteta) števila n, kar pomeni produkt vseh naravnih števil do n vključno.
Naloga 6. Bojana je bila najbolj modra ženska v kraljestvu Neverhood. Imela je 5 bratov, ki jih je nekoč zlobni Čarovnik ujel in zaklenil v svoji palači - vsakega v ločenem prostoru. Na voljo je bilo 5 sob. Bojana je šla pomagat svojim bratom. Uspela je prepričati Čarovnika, da izvede naslednji poskus: Bojana lahko le enkrat napiše številko od 1 do 5 na steno vsake od petih sob. Potem bo Čarovnik razvrstil številke sob v skladu s starostjo bratov Bojane: od številke sobe, kjer sedi starejši brat, do številke sobe, kjer je zaklenjen mlajši brat, in tako dobi petmestno število. (Tokrat je starejši brat sedel v sobi 1, drugi brat je bil v sobi 2, tretji - v sobi 3, četrti - v sobi 4, najmlajši pa je bil v sobi 5, zato je zlobni Čarovnik zabeležil število 12345.). Medtem bo vsak brat prebral številko, napisano na steni svoje sobe, in bo naslednji dan premeščen v sobo s to številko. Potem bo Čarovnik spet na enak način zabeležil petmestno število, naslednji dan bodo bratje premeščeni v sobe glede na številke na steni in tako naprej. Po petih dneh bo Čarovnik prejel 6 petmestnih števil (vključno z prvim: 12345) in če med njimi ne bo nobenega para enakih števil, bodo bratje svobodni.
Pomagajte Bojani napisati številke na stenah sob.
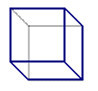
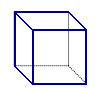
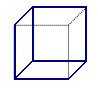
Naloga 7. Z modrim okvirjem so na sliki prikazane vidne ploskve kocke, če jo gledamo od zgoraj desno (glej sliko 1).
Slika 1. Slika 2.
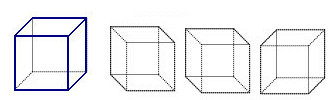
Omejite vidne ploskve preostalih kock, če jih gledamo
а) od spodaj desno;
b) od zgoraj levo;
c) od spodaj levo.
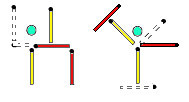
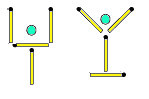
Naloga 8. Tako »čaša« kot »kelih« sta sestavljena iz 4 vžigalic (glej sliko). V vsaki od njih je »češnja«. Za vsako »posodo« premaknite po 2 vžigalici tako, da bosta »češnji« zunaj. (Ne sme biti odvečnih vžigalic.)
Naloga 9. Za okroglo mizo je sedelo 12 ljudi, od katerih je vsak vitez ali oproda. Vitezi vedno govorijo resnico, oprode pa vedno lažejo. Vsak izmed njih je rekel: »Vsi sedeči tukaj, razen mogoče mojih sosedov in mene, so oprode.«
Koliko vitezov je sedelo za mizo?