3 класс
Задача 1. У Миши было 4 карточки со значками (см. рисунок).
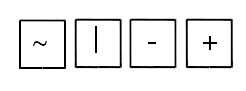
Он решил придумать свои иероглифы, меняя карточки местами так, чтобы каждый иероглиф состоял из четырёх карточек, выложенных в ряд.
Сколько максимум иероглифов может получиться у Миши?
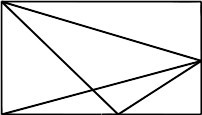
Задача 2. Сколько треугольников на рисунке?
Задача 3. Есть 22 монеты. Известно, что одна монета фальшивая: она легче, чем настоящая. Есть весы, состоящие из двух чаш.

Какое минимальное количество взвешиваний нужно, чтобы определить фальшивую монету?
Задача 4. В одном старинном городе есть парк, а в центре парка — озеро. На озере есть 3 острова. Эти острова соединены с берегом и друг с другом мостами (см. рисунок).
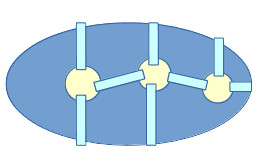
Можно ли пройти по всем мостам, не проходя дважды через один и тот же мост (начинать можно как с берега, так и с любого из островов)? Если да, то как? Если нет, то почему?
Задача 5. На разлинованную доску, состоящую из 9 клеток, села божья коровка (см. рисунок).

Из этой клеточки она выползла, проползла мимо трёх других клеток и остановилась на четвёртой. При этом она могла двигаться только вперёд, назад, влево или вправо (но не по диагонали). Обозначте все клетки, в которых божья коровка могла после этого оказаться.
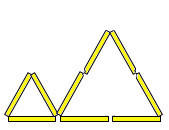
Задача 6. Из 9 палочек сложили 3 треугольника (см. рисунок).
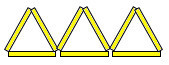
Покажите, как переложить 2 палочки, чтобы получилось 2 треугольника (лишних палочек быть не должно).
Задача 7. Отрезок АВ равен 9 см. На нём поставили точку О так, что отрезок АО получился в 2 раза короче отрезка ОВ. Какова длина АО?
Задача 8. В прихожей стоит 5 велосипедов. Некоторые из них двухколёсные, а некоторые трёхколёсные. Известно, что всего у них 12 колёс. Сколько двухколёсных, а сколько трёхколёсных велосипедов стоит в прихожей? (Задача решается без помощи уравнения.)
Задача 9. На прямом участке дороги длиной 10 километров с одной стороны в ряд расставили фонари (от самого начала дороги до самого её конца). Расстояние между каждыми двумя соседними фонарями равно 1 километру. Сколько фонарей стоит вдоль дороги?
Задача 10. Прилетели птицы и сели на ветки старой берёзы. Если на каждую ветку сядет по 1 птице, то одной птице не достанется места. Если на каждую ветку сядет по 2 птицы, то одна ветка останется пустой. Сколько было птичек, а сколько веток? (Задачу можно решить путём логических рассуждений, без подбора.)
Задача 11. На рисунке 1 показаны фигуры пентамино. Слово пентамино означает, что фигура состоит из 5 одинаковых клеточек.
Рисунок 1
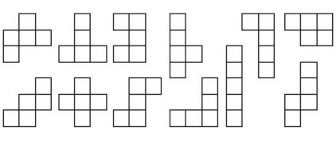
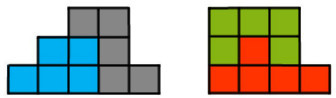
Имеется всего по одной фигурке пентамино каждого вида. Из некоторых из них сложите две фигурки, показанные на рисунке 2. Фигуры пентамино можно поворачивать и/или переворачивать на оборотную сторону (получать зеркальное отображение), но нельзя одну и ту же фигуру использовать дважды! (Даже в перевёрнутом виде.)
Рисунок 2
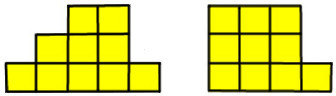
Задача 12. У Оли был большой кубик. Она вырезала из него 4 маленьких кубика (см. Рисунок 1), получившуюся фигуру целиком окунула в краску, после чего сделала отпечатки на бумажном листе. Какие из отпечатков у неё не могли получиться (см. Рисунок 2)?
Рисунок 1

Рисунок 2
Задача 13. Разрежьте фигуру вдоль границ клеточек (см. рисунок) на 3 неравных прямоугольника.

Задача 14. В волшебном лесу жили только зайцы и лисы. Зайцы всегда говорили правду, а лисы всегда лгали. Зайцы боялись лис, но не боялись других зайцев, а лисы никого не боялись. Однажды на поляне вокруг пенька собрались 3 зверя. Каждый зверь посмотрел на своего соседа справа и сказал: «Я тебя боюсь!»
Сколько было зайцев на поляне?