5. razred
Naloga 1. Mina ima 6 različnih majic, 4 različna krila, dvoje hlač in 3 različne obleke. Največ koliko dni zapored se lahko oblači tako, da bo vsak dan izgledala drugačno?
Naloga 2. Mojca in njen oče praznujeta rojstni dan 1. junija. Toda je oče starejši od Mojce za 22 let. Koliko bo star, ko bo trikrat starejši od Mojce?
Naloga 3. Peter in Ivan potujeta z vlakom. Peter sedi v 77. vagonu od začetka vlaka, Ivan pa v 44. od konca. Izkazalo se je, da Ivan in Peter sedita v istem vagonu. Koliko vagonov je v tem vlaku?
Naloga 4. Peter je na list papirja napisal 3 naravna števila. Ivan je seštel vsak par od teh števil in tako dobil 3 različne vsote: 12, 13 in 14. Dokažite, da je Ivan nekje naredil napako.
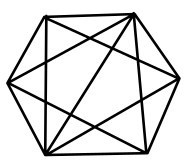
Naloga 5. Koliko trikotnikov je na sliki?
Naloga 6. Sneguljčica je razdelila jabolka med sedem palčkov. Prvi palček je dobil polovico vseh jabolk, ki jih je imela Sneguljčica, drugi palček - polovico preostalih in tako naprej, dokler vsak palček ni dobil jabolk. Eno jabolko je na koncu ostalo za Sneguljčico. Koliko jabolk je imela na začetku?
Naloga 7. Peter in Ivan štejeta drevesa, ki rastejo ob ribniku. Začela sta šteti od različnih dreves, vendar sta se gibala v krogu v isto smer. Tisto drevo, ki je bilo 20. za Petra, je bilo 3. za Ivana in deseto drevo za Petra je bilo 40. za Ivana. Koliko dreves raste ob ribniku?
Naloga 8. Iz 6 vžigalic na ploskvi lahko zložimo samo 1 pravokotnik, ne da bi zlomili nobene vžigalice. Koliko različnih pravokotnikov je mogoče zložiti na ta način, če je vsak pravokotnik sestavljen iz 10 vžigalic?
Naloga 9. Lesena kocka z robom 3 cm je bila popolnoma potopljena v barvo. Ko se je barva na kocki posušila, so jo razrezali na majhne kockice z robom 1 cm.
Koliko kock je na koncu imelo:
a) eno pobarvano ploskev?
b) dve pobarvani ploskvi?
c) tri pobarvane ploskve?
Naloga 10. Poštar pobere pisma iz nabiralnika 5-krat dnevno v enakih časovnih intervalih. Prvič vzame pisma ob 7. uri, zadnjič pa ob 19. uri. Kolikšni so intervali?
Naloga 11. Na sliki 1 so prikazani liki pentamino. Beseda »pentamino« pomeni, da je vsak od teh likov sestavljen iz 5 enakih kvadratkov.
Slika 1
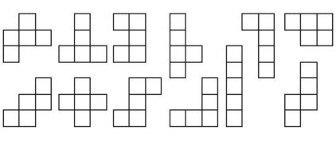
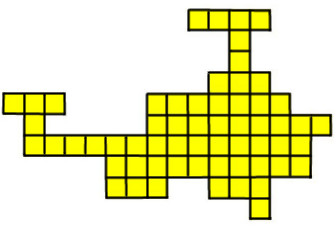
Imamo le en lik pentamino vsake vrste.
Iz njih sestavite podobo helikopterja, ki je prikazana na sliki 2. Pentaminoji lahko vrtite in tudi obračate na hrbtno stran, ampak nobenega lika ne smete uporabiti več kot enkrat (tudi če je obrnjen).
Slika 2
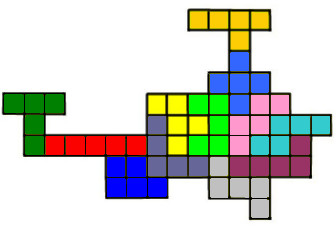
Naloga 12. Na sliki so prikazane sobe v hiši, kjer živi Tanja.
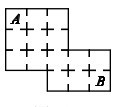
Tanja se sprehaja iz sobe A v sobo B, ne da bi se znašla v eni sobi dvakrat (ni nujno, da gre skozi vse sobe). Koliko različnih poti obstaja, če se sprehodi na tak način?
Naloga 13. Na sliki je kot 30º. Koliko bi meril ta kot, če bi ga gledali skozi 10-kratno povečevalno steklo?

Naloga 14. Na otoku Središče živijo le vitezi in oprode. Oprode vedno lažejo, vitezi pa vedno govorijo samo resnico. Nekoč je za okroglo mizo sedelo 2015 domačinov. Nekateri od njih so rekli: »Moj sosed na desni je oproda!« Katero je največje možno število sedečih za to mizo domačinov, ki bi lahko to rekli?