5 класс
Задача 1. У Маши есть 6 разных футболок, четыре юбки, двое шорт и 3 платья. Сколько дней она может одеваться так, чтобы каждый день выглядеть по-другому, чем в предыдущие дни?
Задача 2. Оля и её папа празднуют день рождения 1 июня. Но папа старше Оли на 22 года. Сколько лет будет папе, когда он будет в 3 раза старше Оли?
Задача 3. Вася едет в поезде в 77 вагоне от начала поезда, а Петя в 44 вагоне от конца поезда. Оказывается, они едут в одном и том же вагоне. Сколько вагонов в поезде?
Задача 4. Вася написал на бумажке 3 натуральных числа. Петя сложил эти числа попарно и получил 3 различные суммы: 12, 13 и 14. Докажите, что Петя где-то ошибся.
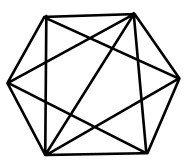
Задача 5. Сколько треугольников на картинке?
Задача 6. Белоснежка раздавала яблоки 7 гномам. Первому она отдала половину всех имеющихся у неё яблок, второму — половину оставшихся, и так далее, пока не раздала всем гномам яблоки. Одно яблоко осталось при этом у Белоснежки. Сколько яблок у неё было сначала?
Задача 7. Петя и Вася считают деревья, растущие вокруг пруда. Они начали счёт с разных деревьев, но движутся по кругу в одном направлении. То дерево, которое Петя посчитал двадцатым, Вася посчитал третьим, а десятое дерево для Пети для Васи оказалось сороковым. Сколько деревьев растёт вдоль пруда?
Задача 8. Из 6 спичек на плоскости можно сложить только 1 прямоугольник. Сколько различных прямоугольников может получиться, если каждый складывать из 10 спичек?
Задача 9. Деревянный кубик с ребром 3 см полностью окунули в краску. Когда краска подсохла, кубик распилили на маленькие кубики с ребром 1 см.
Сколько получилось кубиков:
a) с одной окрашенной гранью?
б) с двумя окрашенными гранями?
в) с тремя окрашенными гранями?
Задача 10. В первый раз почтальон забирает письма из почтового ящика ровно в 7 утра, а в последний раз - в 7 вечера. Всего он забирает письма 5 раз в день через равные промежутки времени. Через какие?
Задача 11. На рисунке 1 показаны фигуры пентамино. Слово пентамино означает, что фигура состоит из 5 одинаковых клеточек.
Рисунок 1
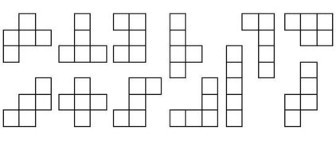
Имеется всего по одной фигуре пентамино каждого вида.
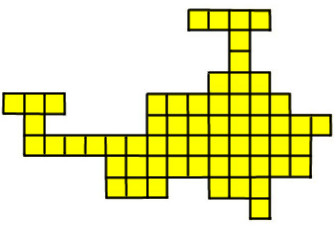
Из них сложите фигурку вертолёта, показанную на рисунке 2. Фигуры пентамино можно поворачивать и/или переворачивать на оборотную сторону (получать зеркальное отображение), но нельзя одну и ту же фигуру использовать дважды! (Даже в перевёрнутом виде.)
Рисунок 2
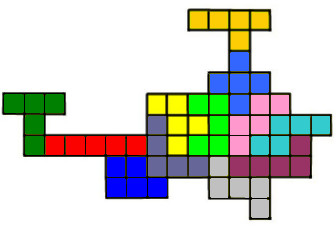
Задача 12. На рисунке показан план дома в Солнечном городе, в котором гостит у своих друзей Незнайка.
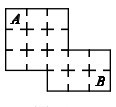
Любые 2 соседние комнаты соединены дверью. Незнайка хочет пройти из своей комнаты (на плане это комната А) в комнату Шпунтика (комната В на плане). Сколькими способами он может это сделать, если не будет дважды проходить через одну и ту же комнату?
Задача 13. На рисунке — угол 30º. Чему будет равен этот угол, если смотреть на него в лупу с 10-кратным увеличением?

Задача 14. На острове Фру-фру живут только лжецы и рыцари. Лжецы всегда лгут, а рыцари всегда говорят только правду. Как-то раз собрались за круглым столом 2015 островитян. Некоторые из них сказали: «Мой сосед справа — лжец!». Какое наибольшее количество сидящих за тем столом островитян могли такое сказать?